Lineare Gleichungssysteme |
8. Klasse Realschule und Gymnasium
|
8. Klasse Realschule und Gymnasium |
|
Frage: Wie löse ich folgende Aufgaben aus dem Themenbereich Zahlenrätsel ? |
||||
| 1. Aufgabe: Die Summe zweier Zahlen beträgt 35. Ihre Differenz ist 17. Lösung: Es können aufgrund der Angaben zwei Gleichungen aufgestellt werden: I ) X + y = 35 II ) x - y = 17 Wir verwenden das Einsetzungsverfahren und stellen die Gleichung zunächst nach x um: x = y + 17 In I) eingesetzt: y + 17 + y = 35 2 y + 17 = 35 / - 17 2 y = 18 /:2 y= 9 In II) x - 9 = 17 / + 9 X = 26 L = {26/9} 2. Aufgabe: Die Summe zweier Zahlen beträgt 69. Ihre Differenz ist 13. Lösung: Es können aufgrund der Angaben zwei Gleichungen aufgestellt werden: I ) X + y = 69 II ) x - y = 13 Wir verwenden das Einsetzungsverfahren und stellen die Gleichung zunächst nach x um: x = y + 13 In I) eingesetzt: y + 13 + y = 69 2 y + 13 = 69 / - 13 2 y = 56 /:2 y= 28 In II) x - 28 = 13 / + 28 X = 41 L = {41/28} 3. Aufgabe: Addiert man zu einer Zahl 5, so erhält man das Vierfache einer zweiten Zahl. Das Doppelte der ersten Zahl, vermindert um 6, ergibt auch das Vierfache der zweiten Zahl. I ) X + 5 = 4 y II ) 2 X - 6 = 4 y Wir stellen zunächst Gleichung I nach X um: I ) X = 4y - 5 Nun setzen wir X = 4y - 5 in Gleichung II ein: 2 (4y -5) - 6 = 4y 8 y - 10 - 6 = 4 y /+ 16 / - 4 y 4 y = 16 /: 4 y = 4 In I ) X + 5 = 4 (4) X + 5 = 16/-5 X = 11 L= {11/4} 4. Aufgabe: Das Doppelte einer Zahl ist um 7 größer als das Dreifache einer zweiten Zahl. Die Summer beider Zahlen ist um 2 kleiner als das Dreifache der zweiten Zahl . Das Aufstellen der Gleichung ist hier nicht ganz einfach !! Folgende Überlegung vorweg: Wenn etwas größer ist, dann müssen wir von dort etwas weg nehmen um Gleichheit zu erhalten. I ) 2X - 7 = 3 y II) x + y + 2 = 3 y / -y/-2 Nach den Rechenschritten ergibt sich folgende vereinfachte Gleichung: II ) x = 2 y - 2 Wir setzen nun X = 2y - 2 in Gleichung I) ein: IN I ) 2 (2y -2) -7 = 3y 4 y - 4 -7 = 3y 4 y -11 = 3y /+11 4 y = 3 y+11 / -3y y = 11 In II ) X = 2 (11) -2 X = 22-2 X = 20 L= {20/11} 5. Aufgabe: Das Produkt aus einer Zahl und 2,5 ist um 8 größer als das Doppelte einer zweiten Zahl. Das Fünffache der zweiten Zahl ist um 2 kliener das das Vierfache der ersten. I) 2, 5 X - 8 = 2 y II) 5 y + 2 = 4X /-2 5 y = 4 X - 2/: 5 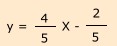 IN I ) eingesetzt:   IN I) 2,5 * (8) -8 = 2y 20 - 8 = 2 y 12 = 2 y / :2 y = 6 L = {8/6} |
|
|||
|
|
|
| Das
Schulportal der Pfalz mit vielen Infos rund um Schule und Studium Lernhilfen, Interpretationshilfen, Lektüren, Kopiervorlagen, Arbeitsmaterialien für die Schule u.v.m. Surftipp: Besuchen Sie doch auch das große Eventportal bzw. die neue Plattform für Englisch Lektüren www.english-readers.de !! |
|